En geometría, un polígono es una figura plana compuesta por una secuencia finita de segmentos rectos consecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices. El interior del polígono es llamado área. El polígono es el caso bidimensional .
La palabra polígono deriva del griego antiguo πολύγωνος (polúgonos), a su vez formado por πολύ (polú) ‘muchos’ y γωνία (gōnía) ‘ángulo’,1 2 3 aunque hoy en día los polígonos son usualmente entendidos por el número de sus lados.
Elementos de un polígono
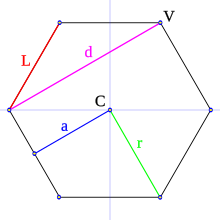
En un polígono se pueden distinguir los siguientes elementos geométricos:
- Lado (L): es cada uno de los segmentos que conforman el polígono.
- Vértice (V): es el punto de intersección (punto de unión) de dos lados consecutivos.
- Diagonal (d): es el segmento que une dos vértices no consecutivos
- Perímetro (P): es la suma de las longitudes de todos los lados del polígono.
- Ángulo interior (AI): es el ángulo formado internamente por dos lados consecutivos.
En un polígono regular se puede distinguir, además:
- Centro (C): es el punto equidistante de todos los vértices y lados.
- Ángulo central (AC): es el formado por dos segmentos de recta que parten del centro a los extremos de un lado.
- Apotema (a): es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
- Diagonales unión de dos vértices no consecutivos por dentro del polígono.
Clasificación
| Clasificación de polígonos según el número de lados | ||
|---|---|---|
| Nombre | n.º lados | |
| trígono, triángulo | 3 | |
| tetrágono, cuadrángulo, cuadrilátero | 4 | |
| pentágono | 5 | |
| hexágono | 6 | |
| heptágono | 7 | |
| octógono u octágono | 8 | |
| eneágono o nonágono | 9 | |
| decágono | 10 | |
| endecágono o undecágono | 11 | |
| dodecágono | 12 | |
| tridecágono | 13 | |
| tetradecágono | 14 | |
| pentadecágono | 15 | |
Los polígonos se clasifican por el número de sus lados según la tabla adjunta, o bien por la forma de su contorno.
|
Un polígono, por la forma de su contorno, se denomina:
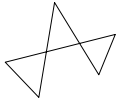
- Simple, si ningún par de aristas no consecutivas se corta.
- Convexo, si al atravesarlo una recta lo corta en un máximo de dos puntos, es el que tiene todos sus ángulos menores que 180º.
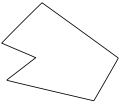
- Cóncavo, si al atravesarlo una recta puede cortarlo en más de dos puntos; es el que tiene uno o varios ángulos mayores que 180º.
- Equilátero, si tiene todos sus lados iguales.
- Regular, si es equilátero y equiángulo a la vez.
- Irregular, si tiene sus ángulos y lados desiguales.
- Estrellado, si se construye a partir de trazar diagonales en polígonos regulares. Se obtienen diferentes construcciones dependiendo de la unión de los vértices: de dos en dos, de tres en tres, etc.


No hay comentarios:
Publicar un comentario